Exploring Our Fluid Earth

Waves

The word wave may bring to mind images of the ocean or a lake, but waves can occur in several different forms. The two main types of waves are mechanical waves and electromagnetic waves. Mechanical waves are disturbances in any medium or substance. Examples of mechanical waves include the movement of water, from ripples in a puddle to giant rolling waves on the surface of the open ocean. A plucked, vibrating guitar string represents a mechanical wave, as does the sound wave it produces by disturbing the air around it.

Electromagnetic waves do not need to move through a substance in order to propagate energy. Electromagnetic waves are disturbances or oscillations in electrical and magnetic fields. Examples of electromagnetic waves include visible light from a streetlamp, ultraviolet light from the sun, and radio waves transmitted and received by a mobile phone. Both mechanical and electromagnetic waves are capable of transferring energy. For example, water waves (mechanical waves) can transfer energy across an entire ocean basin, even though individual water molecules do not travel great distances.

Sources of Waves

Waves are caused by a physical disturbance or vibration. The force of blowing wind is the physical disturbance that generates most water waves. Such waves are termed wind waves. Wind wave patterns change with seasonal wind patterns. For example, during the winter, waves on the northern shores of the Hawaiian Islands can be very large. These large winter waves usually originate from seasonal storms in the North Pacific ocean basin.

Although most water waves are caused by wind, there are other sources of waves. Tsunamis are waves caused by movements of the earth’s crust, such as earthquakes. Tsunamis are unpredictable and can rise unexpectedly from the sea and level whole coastal communities. Tidal waves are caused by the gravity of the moon and the sun. Tidal waves cause water levels in the ocean and lakes to rise and fall on a regular, predictable basis, covering shores during high tide and exposing them during low tide.

Describing Waves

There are different ways to describe the properties of ocean waves, one being surf reports (Table 4.0)

This forecast was produced through the collaborative efforts of the National Weather Service (NWS) and the National Coastal Data Development Center (NCDDC). For additional resources see: http://www.prh.noaa.gov/hnl/pages/marine.php.
NWS Forecaster DONALDSON and Pat Caldwell, Pacific/Hawai‘i Liaison Office, NCDDC

This surf report describes the consistency and size of waves and the wind. The tides are noted because they affect the shape and location of waves. The report also gives a forecast of future wave conditions.

When describing waves that are traveling at a constant rate and not changing significantly over time, scientists often use the terms described in Table 4.1.

Table 4.1. Wave terms and formulas

Crest The highest point of a wave Trough The lowest point of a wave Wave height (H) The vertical distance from crest to trough Amplitude (A) The vertical distance from crest to average surface level or still-water level. Equal to one-half of the wave height. Wavelength (L) The horizontal distance from crest to crest Wave period (T) The time that it takes for one complete wave, from crest to crest to pass a fixed point, usually expressed in seconds per wave. Period is the inverse of frequency.   Thu, 04/16/2015 - 09:41 fyang Wave frequency (F) The number of wave crests that pass a fixed point per unit of time, usually expressed in waves per second. Frequency is the inverse of period.   Thu, 04/16/2015 - 09:41 fyang Wave speed (S) The speed of the wave in a certain direction expressed as distance per unit of time. Wave speed can be calculated by dividing the wavelength of a wave by the period.   Thu, 04/16/2015 - 09:41 fyang Still-water level Water level when the surface is flat and smooth with no waves. Still-water level is slightly lower than halfway between the crest and trough because crests are usually steeper and narrower than troughs. Wave direction If a wave has a speed (S), then wave direction can be noted used compass headings or arrows in a diagram.

Image

Image caption

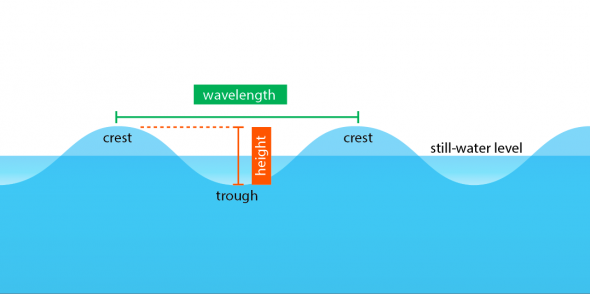
Fig. 4.2. Profile of a standing water wave

Image copyright and source

Image by Byron Inouye

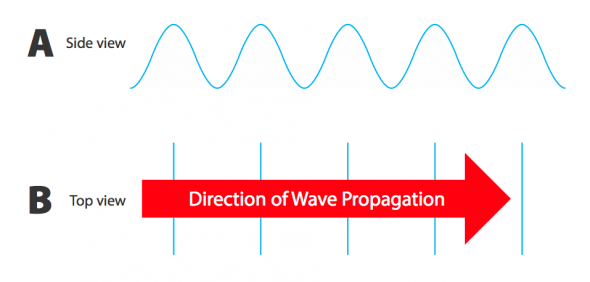
To represent these attributes visually, scientists may use a wave profile diagram (Fig. 4.2). A wave profile is a side view of a wave and is used to show wave features including crests, troughs, wave height, and wavelength. In order to describe a set of waves traveling in a specific direction, scientists use top-view wave diagrams (Fig. 4.3), where vertical lines represent the consecutive troughs or crests of waves. An arrow is used to depict the direction of propagation (movement) of the waves.

Image

Image caption

Fig. 4.3. Diagram showing two views of waves. The side view (A) shows a wave profile with several crests and troughs. The top view (B) shows the same waves with vertical lines representing the wave crests traveling in the direction represented by an arrow.

Image copyright and source

Image by Byron Inouye

Calculating Wave Properties

By mathematically relating wave properties, it is possible to gain valuable information about wave behavior. The basic properties of waves are measurable in units of distance and time. Two properties that can be measured directly are wavelength (L), which is the distance or length from wave crest to wave crest, and period (T), which is the time it takes a wave to pass a fixed point (Fig. 4.2).

Wave Speed

Wave speed is often reported in standard scientific units of meters per second (m/s), but can also be reported in meters per minute (m/min) or other units of distance per unit of time. Knowing wavelength and wave period, the wave speed (S) can be calculated by dividing wavelength (L) by time, or period (T). For example, if a wave has a wavelength of 20 meters and a period of 4 seconds, wave speed can be calculated by dividing 20 m by 4 s, which is equal to 5 m/s.

Wave Period

In order to determine the period of a wave, it is necessary to know the amount of time between waves. Period is usually measured in seconds per wave. To determine period (T), wavelength (L) is divided by speed (S). For example, to find the period of a wave with a speed of 6 m/s and a wavelength of 12 meters, divide the length by the speed; 12 m divided by 6 m/s equals 2 s.

Wave Frequency and Wave Period

To calculate wave frequency and period, it is helpful to remember the inverse relationship between these two properties. Frequency is measured in waves per second and period is measured in seconds per wave. For example, if the period is 2 seconds, then the frequency is 0.5 waves per second.

Standing waves are waves that do not appear to move forward or advance in position. Rather, they oscillate or vibrate in place. A plucked guitar string is an example of a standing mechanical wave with two fixed ends. Standing waves occur when waves with the same frequency, wavelength, and amplitude interact. In contrast to standing waves, transverse waves advance in position. Water waves on the surface of the ocean do not typically behave like standing waves. Instead, they behave like transverse waves, propagating their energy forward as they move.